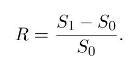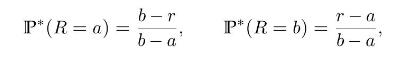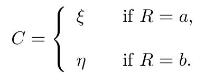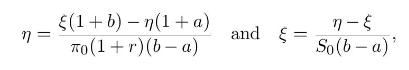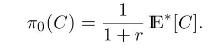Consider a one-step market model with two time instants (t=0) and (t=1) and two assets: - a
Question:
Consider a one-step market model with two time instants \(t=0\) and \(t=1\) and two assets:
- a riskless asset \(\pi\) with price \(\pi_{0}\) at time \(t=0\) and value \(\pi_{1}=\pi_{0}(1+r)\) at time \(t=1\),
- a risky asset \(S\) with price \(S_{0}\) at time \(t=0\) and random value \(S_{1}\) at time \(t=1\).
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Introduction To Stochastic Finance With Market Examples
ISBN: 9781032288277
2nd Edition
Authors: Nicolas Privault
Question Posted: