Sounds are the result of small changes in pressure. To predict the speed at which such disturbances

Question:

Sounds are the result of small changes in pressure. To predict the speed at which such disturbances travel, assume that P, ρ, v, and T in a fluid are each perturbed slightly from their constant values at rest. Denoting the static values by a subscript zero and the time- and position-dependent perturbations by primes, and setting v₀ = 0,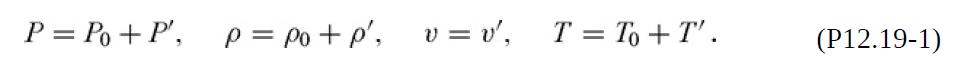

In sound transmission the velocity and temperature gradients are small enough that viscous stresses and heat conduction are each negligible, making the process isentropic. As outlined below, this leads both to Eq. (12.4-1) for c and to the identification of c as a wave speed.

(a) Starting with the time-dependent, one-dimensional continuity and inviscid momentum equations, and assuming that products of primed quantities are negligible, show that

(b) Under isentropic conditions the pressure and density gradients are related as

where the subscript S denotes constant entropy. Use Eq. (12.5-28) and the ideal-gas law to show that (∂P/∂ρ)_S = γRT/M, which has the dimension of velocity squared (L² T⁻²). Because this quantity is positive, it may be denoted as c².

(c) The physical significance of c is revealed by returning to the continuity and momentum equations. Show that they can be combined now to give

A partial differential equation of this form is a wave equation. (The same equation governs v.)

(d) Wave equations are among the most thoroughly studied partial differential equations, but detailed solutions are not needed to interpret c. Show by substitution that Eq. (P12.19-5) has solutions of the form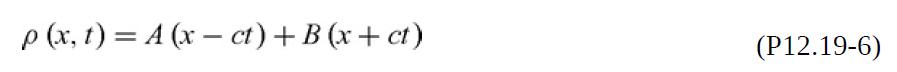

where A and B are any functions that are differentiable. That x and t can be combined into a single variable as x ± ct indicates that c is a wave speed. For example, suppose that ρ(x, t) = A(x − ct) and B = 0. At time t₁ the density at position x₁ is A(x₁ − ct₁). At a later time t₂ that density will be replicated at the position x₂ that keeps the functional argument the same.

That is, x₂ – ct₂ = x₁ − ct₁ or Δx = x₂ – x₁ = c(t₂ – t₁) = c Δt. Because each value of ρ migrates a distance Δx = c Δt in a time Δt, there must be a density wave traveling at speed c in the + x direction, as depicted in Fig. P12.19. Pressure variations accompany density disturbances and therefore travel at the same speed. Similar reasoning shows that B(x + ct) represents waves traveling at speed c in the − x direction.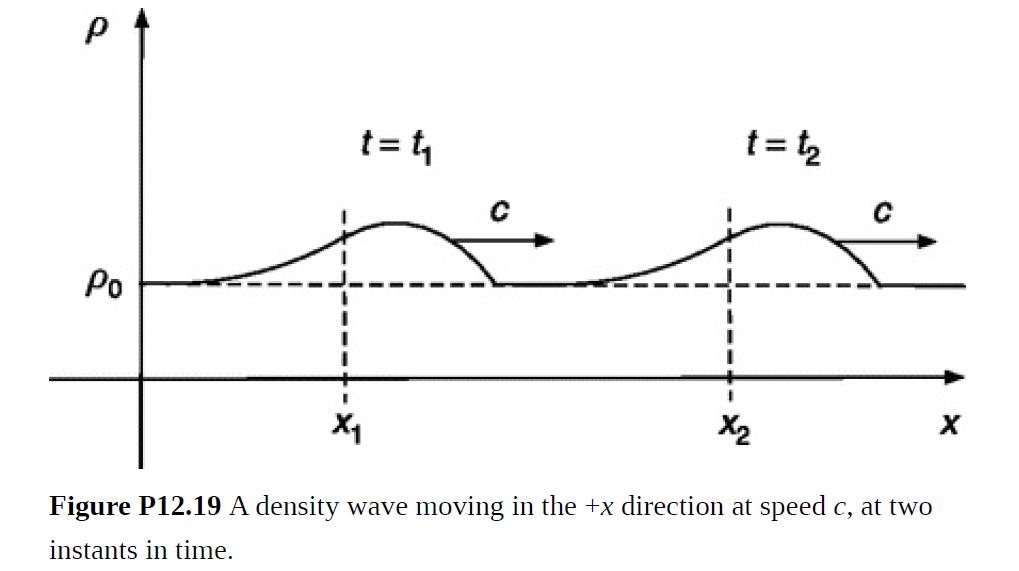

Speeds of sound predicted from Eq. (12.4-1) are typically within 1% of values measured for various gases at atmospheric pressure (Thompson, 1972, p. 165). This confirms that sound transmission is isentropic, rather than isothermal. In a perfectly incompressible fluid, c = ∞. In the above derivation the bulk fluid was assumed to be stationary. More generally, c is the speed of sound relative to the fluid velocity.