Let (left{X_{n}ight}_{n=1}^{infty}) be a sequence of independent and identically distributed random variables following a (operatorname{ChiSquared}(theta)) distribution. In
Question:
Let \(\left\{X_{n}ight\}_{n=1}^{\infty}\) be a sequence of independent and identically distributed random variables following a \(\operatorname{ChiSquared}(\theta)\) distribution. In Example 7.12 we derived a saddlepoint expansion that approximates the density of \(n \bar{X}_{n}\) at a point \(x\) with relative error \(O\left(n^{-1}ight)\) as \(n ightarrow \infty\), given by
\(f_{n}(x)=\left[4 \pi n^{-1} x^{2} \thetaight]^{-1 / 2} \exp \left[-\frac{1}{2} n \theta \log \left(n \theta x^{-1}ight)-\frac{1}{2}\left(1-n x^{-1} \thetaight)ight]\left[1+O\left(n^{-1}ight)ight]\).
Prove that an application of Theorem 1.8 (Stirling) implies that the leading term of this expansion has the same form as a GAMma distribution.

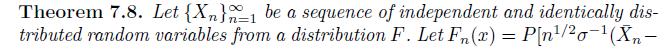
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





