By applying the following transformation on the dependent variable in the BlackScholes equation while the auxiliary conditions
Question:
By applying the following transformation on the dependent variable in the Black–Scholes equation
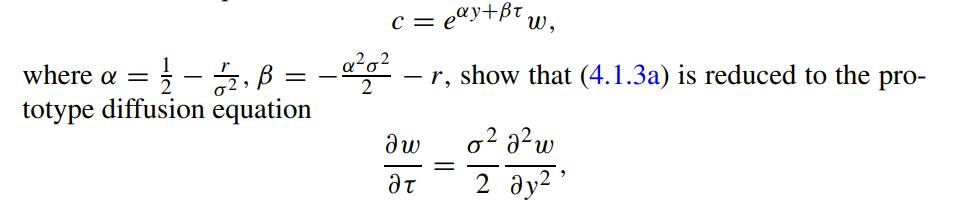
while the auxiliary conditions are transformed to become
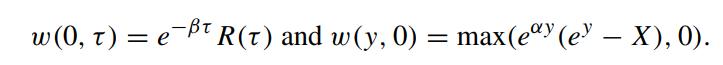
Consider the following diffusion equation defined in a semi-infinite domain
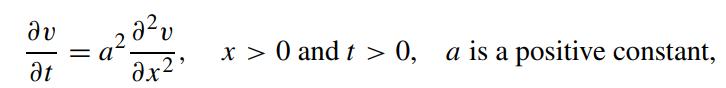
with initial condition: v(x, 0) = f (x) and boundary condition: v(0,t) = g(t), the solution to the diffusion equation is given by (Kevorkian, 1990)
![1 2a /1 * (E) [e-x - 5)/41 _ e-(x+8}/4"}d} S (x+)/4at] Jo v(x, t) = pt e-x/4aw 63/2 X 20 7 So + -g(t - w)](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/4/8/2/096655b4c30256fb1700482093066.jpg)
Using the above form of solution, show that the price of the European downand-out call option is given by
![1 2 Jo [e-(y-)/207 - e-(x+4)/20 + ]d c(y, t) = eay+Bt So max(e-a (e X), 0) pt e-B(t-w)e-y/20 w R(t w) dw}.](https://dsd5zvtm8ll6.cloudfront.net/images/question_images/1700/4/8/2/124655b4c4c77bc31700482121405.jpg)
Assuming B
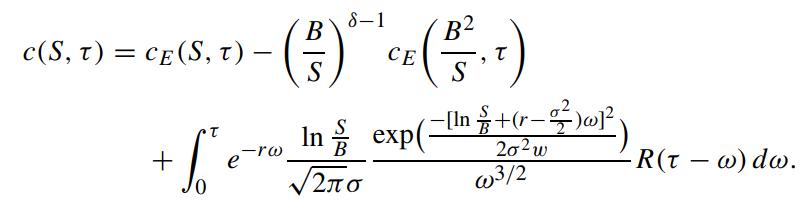
The last term represents the additional option premium due to the rebate payment.
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





