The grand partition function of a gaseous system composed of mutually interacting, spin-half fermions has been evaluated by Lee and Yang (1957), with the result \({ }^{27}\)
\[
\begin{aligned}
\ln \mathcal{Q} \equiv \frac{P V}{k T}=\frac{V}{\lambda^{3}}[ & 2 f_{5 / 2}(z)-\frac{2 a}{\lambda}\left\{f_{3 / 2}(z)ight\}^{2} \\
& \left.+\frac{4 a^{2}}{\lambda^{2}} f_{1 / 2}(z)\left\{f_{3 / 2}(z)ight\}^{2}-\frac{8 a^{2}}{\lambda^{2}} F(z)+\cdotsight]
\end{aligned}
\]

where \(z\) is the fugacity of the actual system (not of the corresponding noninteracting system, which was denoted by the symbol \(z_{0}\) in the text); the functions \(f_{v}(z)\) and \(F(z)\) are defined in a manner similar to equations (11.7.10) and (11.7.24). From this result, one can derive expressions for the quantities \(E(z, V, T)\) and \(N(z, V, T)\) by using the formulae

Data From Equation (11.7.10)

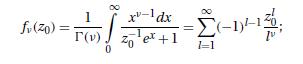
Data From Equation (11.7.24)

\[
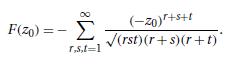
E(z, V, T) \equiv k T^{2} \frac{\partial(\ln \mathcal{Q})}{\partial T} \quad \text { and } \quad N(z, V, T) \equiv \frac{\partial(\ln \mathcal{Q})}{\partial(\ln z)}\left\{=\frac{2 V}{\lambda^{3}} f_{3 / 2}\left(z_{0}ight)ight\}
\]
(a) Eliminating \(z\) between these two results, derive equation (11.7.25) for \(E\).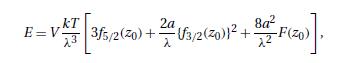
(b) Obtain the zero-point value of the chemical potential \(\mu\), correct to second order in \((a / \lambda)\), and verify, with the help of equations (11.7.31) and (11.7.32), that

Data From Equations (11.7.31) and (11.7.32)

\[
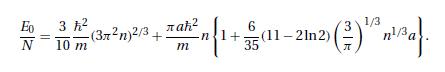
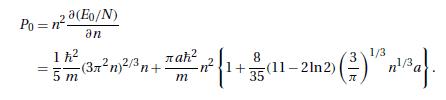
(E+P V)_{T=0}=N(\mu)_{T=0}
\]
[At \(T=0 \mathrm{~K}, \mu=(\partial E / \partial N)_{V}\).]
(c) Show that the low-temperature specific heat and the low-temperature entropy of this gas are given by (see Pathria and Kawatra, 1962)
\[
\frac{C_{V}}{N k} \simeq \frac{S}{N k} \simeq \frac{\pi^{2}}{2}\left(\frac{k T}{\varepsilon_{F}}ight)\left[1+\frac{8}{15 \pi^{2}}(7 \ln 2-1)\left(k_{F} aight)^{2}+\cdotsight]
\]
where \(k_{F}=\left(3 \pi^{2} night)^{1 / 3}\). Clearly, the factor within square brackets is to be identified with the ratio \(m^{*} / m\); see equations (11.8.12) and (11.8.26).

Equation (11.8.12) and (11.8.26)

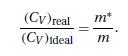
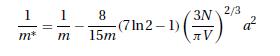
[To determine \(C_{V}\) to the first power in \(T\), we must know \(E\) to the second power in \(T\). For this, we require higher-order terms of the asymptotic expansions of the functions \(f_{v}(z)\) and \(F(z)\); these are given by
\[
\begin{aligned}
& f_{5 / 2}(z)=\frac{8}{15 \sqrt{ } \pi}(\ln z)^{5 / 2}+\frac{\pi^{3 / 2}}{3}(\ln z)^{1 / 2}+O(1) \\
& f_{3 / 2}(z)=\frac{4}{3 \sqrt{ } \pi}(\ln z)^{3 / 2}+\frac{\pi^{3 / 2}}{6}(\ln z)^{-1 / 2}+O(\ln z)^{-5 / 2} \\
& f_{1 / 2}(z)=\frac{2}{\sqrt{ } \pi}(\ln z)^{1 / 2}-\frac{\pi^{3 / 2}}{12}(\ln z)^{-3 / 2}+O(\ln z)^{-7 / 2}
\end{aligned}
\]
and
\[
\begin{aligned}
F(z)= & \frac{16(11-2 \ln 2)}{105 \pi^{3 / 2}}(\ln z)^{7 / 2} \\
& -\frac{2(2 \ln 2-1)}{3} \pi^{1 / 2}(\ln z)^{3 / 2}+O(\ln z)^{5 / 4}
\end{aligned}
\]
The first three results here follow from the Sommerfeld lemma (E.17); for the last one, see Yang (1962).]

Transcribed Image Text:

0 -1dx fv (20) =(-1) (v) zoex +1 1=1