Explore how pulsar timing can be used to detect a plane gravitational wave.

(a) Derive Eq. (27.97).

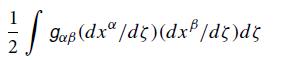
that underlies the rays’ super-hamiltonian; Ex. 25.7. The numerical value of the action is zero, and since it is an extremum along each true ray, if you evaluate it along a path that is a straight line in the TT coordinate system instead of along the true ray, you will still get zero at first order in h_o.]

(b) Recognizing local and pulsar contributions to the timing residuals, explain how much information about the amplitude, direction, and polarization of a gravitational wave from a single black-hole binary can be obtained using accurate timing data from one, two, three, four, and many pulsars.

(c) Suppose, optimistically, that 30 pulsars will be monitored with timing accuracy ∼100 ns, and that arrival times will be measured 30 times a year. Make an estimate of the minimum measurable amplitude of the sinusoidal residual created by a single binary as a function of observing duration and wave frequency f.

(d) Using the result from part (c) and using the predicted residual averaged over the direction and the orientation of the source from Eqs. (27.71c) and (27.71d), estimate the maximum distance to which an individual source could be detected as a function of the chirp mass M and the frequency f.

Equations.

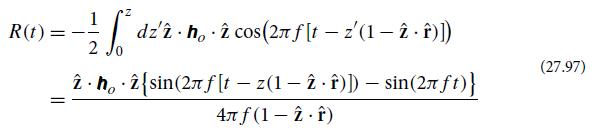
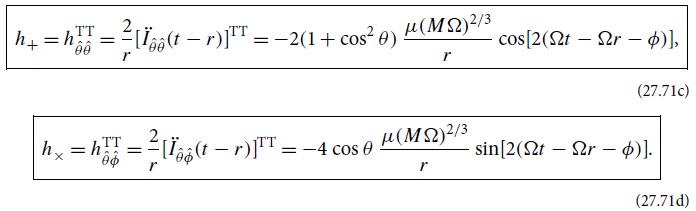
Data from Exercises 25.7.

(a) Show that, among all curves P(ζ) that could take a particle from event P₀ = P(0) to event P₁ = P(ζ₁) (for some ζ₁), those that satisfy the action principle

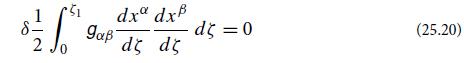
are geodesics, and ζ is the affine parameter along the geodesic related to the particle’s 4-momentum by p(vector) = d/dζ. 

(b) The lagrangian L(x^μ, dx^μ/dζ) associated with this action principle is 1/2g_αβ(dx^α/dζ)(dx^β/dζ),where the coordinates {x⁰, x¹, x², x³} appear in the metric coefficients and their derivatives appear explicitly. Using standard principles of Hamiltonian mechanics, show that the momentum canonically conjugate to x^μ is p_μ = g_μνdx^ν/dζ—which in fact is the covariant component of the particle’s 4-momentum. Show, further, that the hamiltonian associated with the particle’s lagrangian is

Explain why this guarantees that Hamilton’s equations dx^α/dζ = ∂H/∂p_α and dp_α/dζ = −∂H/∂x^α are satisfied if and only if x^α(ζ) is a geodesic with affine parameter ζ and p_α is the tangent vector to the geodesic.

(c) Show that Hamilton’s equations guarantee that, if the metric coefficients are independent of some coordinate x^A, then p_A is a conserved quantity. This is the same conservation law as we derived by other methods.

H = 1/2g^μνp_μp_ν is often called the geodesic’s super-hamiltonian. It turns out that, often, the easiest way to compute geodesics numerically (e.g., for particle motion around a black hole) is to solve the super-hamiltonian’s Hamilton equations.

Transcribed Image Text:

Sp(Sp/gxp) (SP/xp) 86 T S