In Problem 4.1 we showed that the martingale method for portfolio choice can be applied to static incomplete market settings under the special assumption of quadratic utility. Cochrane (2014) extends this method to study intertemporal portfolio choice under incomplete markets by treating dates and states of nature symmetrically. This approach contrasts with the standard approach to intertemporal portfolio choice because it characterizes the investor's optimal stream of final payoffs, that is, the ultimate dividend stream that the investor receives from financial markets, without specifying the dynamic portfolio strategy that supports these payoffs in a given market structure.

Consider the following generalization of the setting of Problem 4.1. A payoff \(X=\) \(\left\{X_{t}ight\}_{t=1}^{\infty} \in \Xi\) now denotes the stream of dividends purchased at price \(P(X)=P\left(\left\{X_{t}ight\}ight)\) at time 0 . The intertemporal analog of payoff returns is the payoff yield, \(Y=X / P(X)\), the stream of dividend yields or coupon rates that correspond to payoff \(X\).

Following Hansen (1987), define a generalized "long-run expectation" operator \(\tilde{\mathrm{E}}[\cdot]\) that sums over time, weighted by a number \(\beta

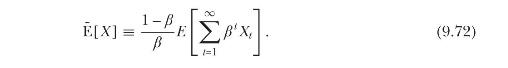
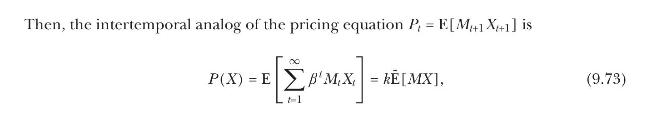
where \(k \equiv \beta /(1-\beta)\). Under this generalized notion of the expectation operator all results derived for the static framework of Problem 4.1 directly carry over to the corresponding infinite-horizon framework and, once again, do not hinge on a particular payoff distribution.

(a) Define the riskfree yield as \(Y_{f}=1 / P(1)\). What is the riskfree asset corresponding to this definition?

(b) Reinterpret the results from Problem 4.1 to conclude that the yield to the optimal payoff of an infinite-horizon quadratic-utility investor with only financial wealth is a linear and time-invariant combination of two yields: the riskfree yield and a longrun mean-variance efficient yield. Moreover, these two yields are the same regardless of the agent's risk aversion. Why do hedging demands and state variables affecting investment opportunities not appear in this characterization?

(c) Cochrane (2014) argues that a focus on final payoffs in asset management can be welfare improving, as it helps separate the investor's risk and return decisions from the financial engineering of how to achieve optimal portfolios in a given market structure. Individual investors will be better served if they focus on specifying the payout streams that are optimal for them and leave the dynamic portfolio implementation of these payoffs to the professional asset management industry. Evaluate this claim.

Data from problem 4.1

The martingale method for portfolio choice, introduced in section 4.1.5, uses the SDF framework to characterize the optimal state-contingent payoffs that agents can attain through financial markets, given their wealth and asset prices, the latter summarized through the SDF. 

Consider an economy with two dates, \(t=0,1\). At date 0 an agent with wealth \(W\) solves the following optimization problem over his date-1 payoff:
\[
\begin{equation*}
\max _{X \in \Xi} \mathrm{E}[u(X)] \quad \text { s.t. } W=P(X)=\mathrm{E}[M X] \text {. } \tag{4.105}
\end{equation*}
\]
Assume that a riskfree asset is traded, \(1 \in \Xi .{ }^{14}\)

Transcribed Image Text:

E[X] = x]. (9.72)