Consider the transition matrix

(a) Argue why in this case we should not hope for ergodicity. How does the chain evolve in this case? Show that Doeblin’s condition of Theorem 4 does not hold for this matrix.

(b) Let (π₀, π₁) and (˜ π₀,˜ π₁) be the stationary distributions for the two-state chains with the transition matrices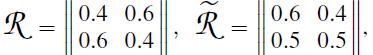

respectively. Argue that these distributions are also the limiting distributions for the two-state chains mentioned.

(c) For α ∈ [0,1], let the vector π(α) = α(π₀, π₁, 0, 0)+(1−α)(0, 0, ˜ π₀, ˜ π₁). Show that for any α ∈ [0,1], the distribution π(α) is stationary for the original chain.

(d) Let the initial distribution π0 = (π₀₀, π₀₁, π₀₂, π₀₃), and α = π₀₀ +π₀₁, the probability that the original chain started in one of the first two states. Show that π_t, the distribution of the chain, converges to π_(α).

(e) Explain all the facts above from a heuristic point of view. The main point is that the sets of states {0,1} and {2,3} do not communicate; that is, the process starting in the set {0,1} will never leave this set, and the same concerns {2,3}.