In this exercise, we continue the study of the two-state system introduced in Example 3.4. Recall that
Question:
In this exercise, we continue the study of the two-state system introduced in Example 3.4. Recall that \(|1angle\) and \(|2angle\) are energy eigenstates with energies \(E_{1}\) and \(E_{2}\), respectively, which are orthonormal: \(\langle i \mid jangle=\delta_{i j}\). The initial state is
\[\begin{equation*}|\psiangle=\alpha_{1}|1angle+\alpha_{2}|2angle \tag{3.164}\end{equation*}\]
where \(\alpha_{1}, \alpha_{2}\) are some complex coefficients.
(a) Calculate the expectation value of the Hamiltonian \(\hat{H}\) from Eq. (3.122) in the time-dependent state \(|\psi(t)angle,\langle\psi(t)|\hat{H}| \psi(t)angle\). Does it depend on time?
(b) Let's assume that there is some other Hermitian operator on this Hilbert space, called \(\hat{\mathcal{O}}\). We know its action on the energy eigenstates:
\[\begin{equation*}\hat{\mathcal{O}}|1angle=|1angle-|2angle, \quad \hat{\mathcal{O}}|2angle=-|1angle+|2angle . \tag{3.165}\end{equation*}\]
Express \(\hat{\mathcal{O}}\) in both bra-ket notation and familiar matrix notation. Is it actually Hermitian?
(c) What is the expectation value of the unitary operator \(\hat{\mathcal{O}}\) from part (b), \(\langle\psi(t)|\hat{\mathcal{O}}| \psi(t)angle\) ? Does it depend on time? What does it simplify to if both \(\alpha_{1}\) and \(\alpha_{2}\) are real?
Example 3.4.
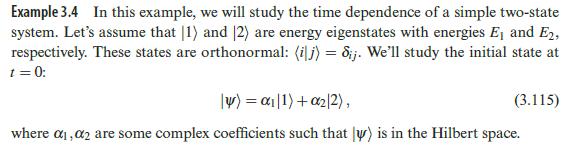
Step by Step Answer:

Quantum Mechanics A Mathematical Introduction
ISBN: 9781009100502
1st Edition
Authors: Andrew J. Larkoski





