When n is large, n! can be approximated by means of the expression Called Stirlings formula, where

Question:

When n is large, n! can be approximated by means of the expression

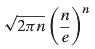
Called Stirling’s formula, where e is the base of natural logarithms. (A derivation of this formula may be found in the book by W. Feller cited among the references at the end of this chapter.)

(a) Use Stirling’s formula to obtain approximations for 10! and 12!, and find the percentage errors of these approximations by comparing them with the exact values given in Table VII.

(b) Use Stirling’s formula to obtain an approximation for the number of 13-card bridge hands that can be dealt with an ordinary deck of 52 playing cards.