The golden ratio is = (1 + 5)/2. John Putz, a mathematician who was interested in

The “golden ratio” is φ = (1 + √5)/2. John Putz, a mathematician who was interested in music, analyzed Mozart’s sonata movements, which are divided into two distinct sections, both of which are repeated in performance (see References). The length of the “Exposition” in measures is represented by a and the length of the “Development and Recapitulation” is represented by b. Putz’s conjecture was that Mozart divided his movements close to the golden ratio. That is, Putz was interested in studying whether a scatter plot of a + b against b not only would be linear, but also would actually fall along the line y = φx. Here are the data in tabular form, in which the first column identifies the piece and movement by the Köchel cataloging system:

(a) Find the equation of the least squares regression line. Superimpose it on the scatter plot.

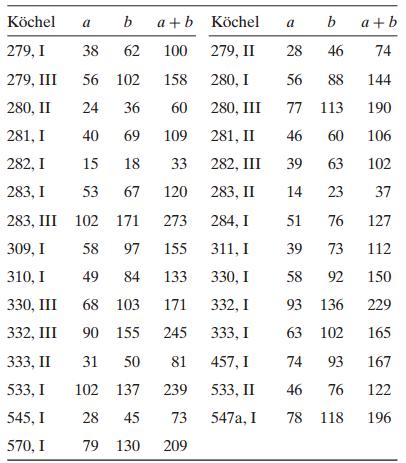
(b) On the scatter plot, superimpose the line y = φx. Compare this line with the least squares regression line (graphically if you wish).

(c) Find the sample mean of the points (a + b)/b. Is the mean close to φ?

Transcribed Image Text:

Köchel ab a+b Köchel a b a + b 279,I38 62 100 279, II 28 46 74 279, III 56 102 158 280, I 56 88 144 280, II 2436 60 280, III 77 113 190 281,I 40 69 109 28, II 46 60 106 282,I 15 18 33 282, II 39 63 102 283,I 53 67 120 283, II 14 2337 283, III 102 171 273 284, I 51 76 127 309, I 58 97 155 31,I 39 73 112 310,I 49 84 133 330,I 58 92 150 330, II 68 103 171 332,I 93 136 229 332, III 90 155 245 333,I 63 102 165 333, II 31 50 8 457, I 74 93 167 533,I 102 137 239 533, II 46 76 122 545,I 28 45 73 547a, 78 118 196 570, I 79 130 209 2