Let (left{X_{n}ight}_{n=1}^{infty}) be a sequence of independent and identically distributed random variables following an EXPONENTIAL(1) density. a.
Question:
Let \(\left\{X_{n}ight\}_{n=1}^{\infty}\) be a sequence of independent and identically distributed random variables following an EXPONENTIAL(1) density.
a. Prove that if \(\tilde{\lambda}=x^{-1}(x-n)\) then \(n c^{\prime}(\tilde{\lambda})=x\).
b. Prove that \(c(\tilde{\lambda})=\log \left(n^{-1} xight)\) and that \(c^{\prime \prime}(\tilde{\lambda})=n^{-2} x^{2}\).
c. Prove that the leading term of the saddlepoint expansion for \(f_{n}(x)\) is given by \((2 \pi)^{-1 / 2} n^{-n+1 / 2} x^{n-1} \exp (n-x)\).
d. The exact form for \(f_{n}(x)\) in this case is \(x^{n-1} \exp (-x) / \Gamma(n)\). Approximate \(\Gamma(n)\) using Theorem 1.8 (Stirling), and show that the resulting approximation matches the saddlepoint approximation.
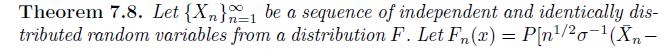
Fantastic news! We've Found the answer you've been seeking!
Step by Step Answer:
Related Book For 

Question Posted:





