Prove the following variants of the Markov inequality Proposition 11.5 . For all (alpha, c>0) and whenever

Question:

Prove the following variants of the Markov inequality Proposition 11.5 . For all $\alpha, c>0$ and whenever the expressions involved make sense/are finite,

(i) $\mu\{|u|>c\} \leqslant \frac{1}{c} \int|u| d \mu$

(ii) $\mu\{|u|>c\} \leqslant \frac{1}{c^{p}} \int|u|^{p} d \mu$ for all \(0

(iii) $\mu\{|u| \geqslant c\} \leqslant \frac{1}{\phi(c)} \int \phi(|u|) d \mu$ for $\phi: \mathbb{R}_{+} ightarrow \mathbb{R}_{+}$increasing;

(iv) $\mu\left\{u \geqslant \alpha \int u d \muight\} \leqslant \frac{1}{\alpha}$ for $u \geqslant 0$;

(v) \(\mu\{|u|

(vi) $\mathbb{P}(|\xi-\mathbb{E} \xi| \geqslant \alpha \sqrt{\mathbb{V} \xi}) \leqslant \frac{1}{\alpha^{2}}$, where $(\Omega, \mathscr{A}, \mathbb{P})$ is a probability space, $\xi$ is a random variable (i.e. a measurable function $\xi: \Omega ightarrow \mathbb{R}$ ), $\mathbb{E} \xi=\int \xi d \mathbb{P}$ is the expectation or mean value and $\mathbb{V} \xi=\int(\xi-\mathbb{E} \xi)^{2} d P$ is the variance.

Remark. This is Chebyshev's inequality.

Data from preposition 11.5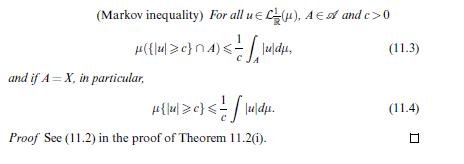

$(Markov inequality) For all u H({\\\c} \4) 0 \d, H{\u\>c}$