Let (left(B_{t} ight)_{t geqslant 0}) be a (mathrm{BM}^{1}) and denote by (g_{t}) the last zero before time
Question:
Let \(\left(B_{t}\right)_{t \geqslant 0}\) be a \(\mathrm{BM}^{1}\) and denote by \(g_{t}\) the last zero before time \(t>0\).
a) Use Theorem 11.25 to give a further proof of Lévy's arc-sine law (cf. Theorem 6.20): \(\mathbb{P}\left(g_{t})=\frac{2}{\pi} \arcsin \sqrt{\frac{s}{t}}\) for all \(s \in[0, t]\).
b) Find the conditional density \(\mathbb{P}\left(\left|B_{t}\right| \in d y \mid g_{t}=s\right)\).
c) Integrate the formula appearing in Theorem 11.25 to get
\[\sqrt{\frac{2}{\pi t}} \exp \left(-\frac{y^{2}}{2 t}\right)=\int_{0}^{t} \sqrt{\frac{2}{\pi s}} \frac{y}{\sqrt{2 \pi(t-s)^{3}}} \exp \left(-\frac{y^{2}}{2(t-s)}\right) d s\]
and give a probabilistic interpretation of this identity.
Data From 11.25 Theorem
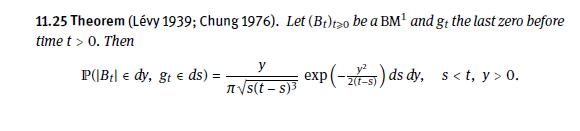

Step by Step Answer:

Brownian Motion A Guide To Random Processes And Stochastic Calculus De Gruyter Textbook
ISBN: 9783110741254
3rd Edition
Authors: René L. Schilling, Björn Böttcher





