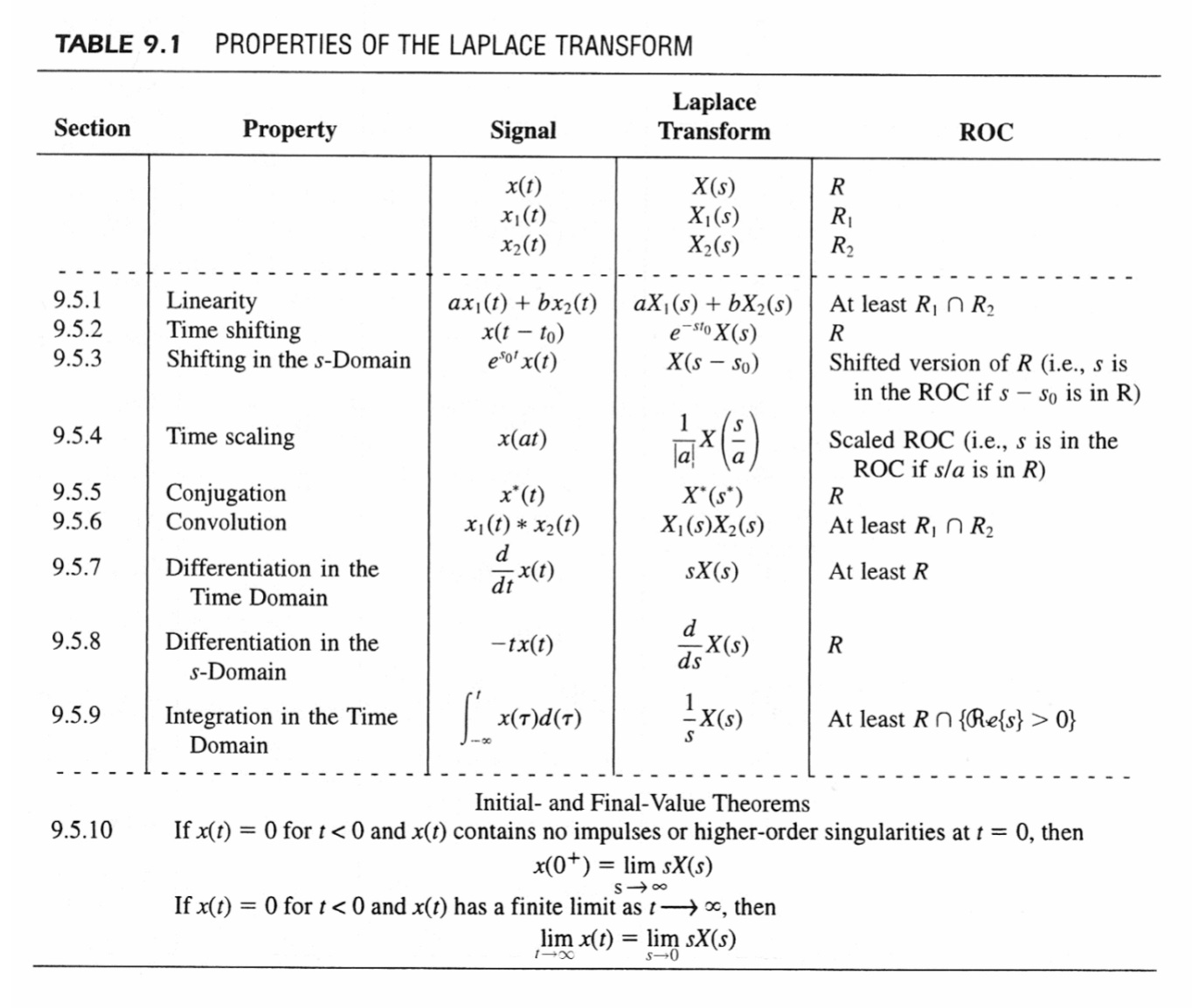
Question: Signals and Systems Laplace Transform Support Material: Transform table for reference TABLE 9.1 PROPERTIES OF THE LAPLACE TRANSFORM Laplace Section Property Signal Transform ROC x(1)
Signals and Systems
Laplace Transform
Support Material: Transform table for reference

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


