(a) Carry through the argument in Sect. 8.1.2, starting with Eq. 8.6, but using Jf in place of J. Show that the Poynting vector becomes S = E x H, and the rate of change of the energy density in the fields is For linear media, show that

(b) In the same spirit, reproduce the argument in Sect. 8.2.2, starting with Eq. 8.15, with, p f and Jf in place of p and J. Don't bother to construct the Maxwell stress tensor, but do show that the momentum density is

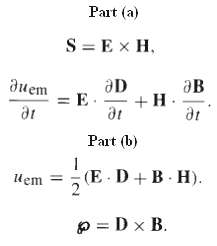
31 lem = Part (a) S = Ex H, D t Part (b) (E.D + B.H). 2 = D x B. = E. t +H