Question: In this problem we illustrate the concepts of sampling and decimation for discretetime signals. To this end consider a signal x(n) with Fourier transform X()
In this problem we illustrate the concepts of sampling and decimation for discretetime signals. To this end consider a signal x(n) with Fourier transform X(ω) as in Figure.
(a) Sampling x(n) with a sampling period D = 2 results to the signal. Compute and sketch the signal xs(n) and its Fourier transform Xs(ω). Can we reconstruct x(n) from xs(n)? How?
(b) Decimating x(n) by a factor of D = 2 produces the signal
xd(n) = x(2n) all n
Show that Xd(ω) = Xs(ω/2). Plot the signal xd(n) and its transform Xd(ω). Do we lose any information when we decimate the sample signal xs(n)?
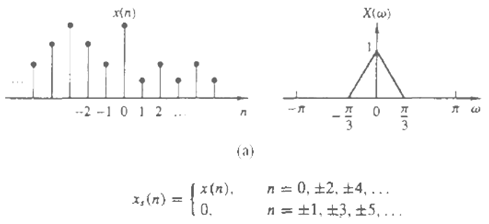
x{) ) --2 -1 0 1 2 . - (a) |x (). (0. 0, +2. +4,... = { , () +1, +3, +5, ...
Step by Step Solution
3.37 Rating (156 Votes )
There are 3 Steps involved in it
a To recover xn from x s n see figure b Since x s n ... View full answer

Get step-by-step solutions from verified subject matter experts
Document Format (1 attachment)
31-E-T-E-D-S-P (912).docx
120 KBs Word File


