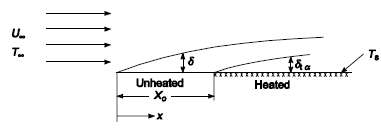
A fluid at temperature T?? is flowing at a velocity U?? over a flat plate which is at the same temperature as the fluid for a distance x0 from the leading edge, but at a higher temperature Ts beyond this point. Show by means of the integral boundary-layer equations that ζ, the ratio of the thermal boundary-layer thickness to the hydrodynamic boundary-layer thickness, over the heated portion of the plate is approximately

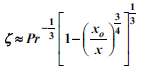
if the flow is laminar.GIVENLaminar flow over a flat plateFluid temperature = T??Fluid velocity = U??Plate temperature = T?? for x Plate temperature = Ts for x > XoASSUMPTIONSSteady stateThe temperature distribution is a third-order polynomial: T ?? Ts = αy + cy3Property value changes due to the temperature profile do not affect the hydrodynamic boundary layer.

5 Pr 3 L X U.. T.. 18 Unheated Xo X t&a Heated To