(a) From the electric dipole fields with general time dependence of Problem 9.6, show that the total power and the total rate of radiation of angular momentum through a sphere at large radius r and time t are

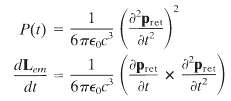
where the dipole moment p is evaluated at the retarded time t = t ? r/c.

(b) The dipole moment is caused by a particle of mass m and charge e moving nonrelativistically in a fixed central potential V(r). Show that the radiated power and angular momentum for such a particle can be written as

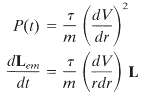
where ? = ?²/6??₀m?³ (= 2e²/3mc³ in Gaussian units) is a characteristic time, L is the particle's angular momentum, and the right-hand sides are evaluated ?at the retarded time. Relate these results to those from the Abraham-Lorentz equation for radiation damping [Section 16.2].

(c) Suppose the charged particle is an electron in a hydrogen atom. Show that the inverse time defined by the ratio of the rate of angular momentum radiated to the particle's angular momentum is of the order of ?⁴c/?₀, where a = e²/4??₀hc ? 1/137 is the fine structure constant and a₀ is the Bohr radius. How does this inverse time compare to the observed rate of radiation in hydrogen atoms?

(d) Relate the expressions in parts a and b to those for harmonic time dependence in Problem 9.8.

aPret P(t) Pret at oPret dLem 6 dt