A modified Bessel-Fourier series on the interval 0 ? ? ? a for an arbitrary function f?(?) can be based on the "homogeneous" boundary conditions:

The first condition restricts v. The second condition yields eigenvalues k = y_vn/a, where y_vn is the nth positive root of x dJ_v(x)/dx + ? J_v(x) = 0.

(a) Show that the Bessel functions of different eigenvalues are orthogonal in the usual way.

(b) Find the normalization integral and show that an arbitrary function f (?) can be expanded on the interval in the modified Bessel-Fourier series

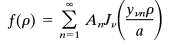
With the coefficients A_n given by

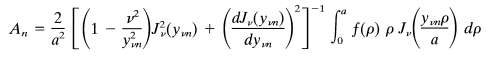
The dependence on ? is implicit in this form, but the square bracket has alternative forms:

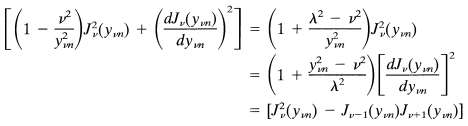
For ? ? ? we recover the result of (3.96) and (3.97). The choice ? = 0 is another simple alternative.

dJ,(k'p) dp At p = 0, pJ,(kp) In[J,(kp)] dp (A real) At p = a,