A player confronts the following situation. A coin will be tossed at every time t, t = 1, 2, 3, . ., T and the player will get a total reward W1,. He or she can either decide to step or to continue to play. If he or she continues, a mew coin ill be tossed at time t + 1, and so on. The question is, what is the best time to stop? We consider several cases. We begin with the double-or-nothing game. The total reward received at time t = T is given by:

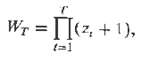
where the z1, is a binomial random variable:Thus, according to this, the reward either doubles or becomes zero at eve-y stage.(a) Can you calculate the expected reward at time T, E[WT], given this information?(b) What is the best time to stop this game?(c) Suppose now we sweeten the reward at every stage and we multiply the WT, by a number that increases and is greater than one. In fact suppose the reward is now given by:

with T = 1, 2, 3,....Show that the expected reward if we stop at some time Tk is given by 2k/k+1.(Here Tk is a stopping time such that one stops after the kth toss.)(d) What is the maximum value this reward can reach?(e) Is there an optimal stoppingrule?

= [e Wr =| (z, + 1), tal