(a) Show that for arbitrary initial polarization, the scattering cross section of a perfectly conducting sphere of radius a, summed over outgoing polarizations, is given in the long-wavelength limit by

Where n₀ and n are the directions of the incident and scattered radiations, respectively, while ?₀ is the (perhaps complex) unit polarization vector of the incident radiation (?₀^* ? ?₀ = 1; n₀ ? ?₀ = 0).

(b) If the incident radiation is linearly polarized, show that the cross section is

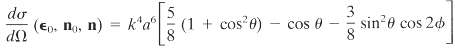
Where n ? n₀ = cos ? and the azimuthal angle ? is measured from the direction of the linear polarization.

(c) What is the ratio of scattered intensities at ? = ?/2, ? = 0 and ? = ?/2 ? = ?/2? Explain physically in terms of the induced multipoles and their radiation patterns.

do k*a* (En, na, n) 5 (n, x n) - ng