a) Suppose that 0 < y < 1/10 n for some integer n > 0. Prove that there is an integer 0 < w <

a) Suppose that 0 y n for some integer n > 0. Prove that there is an integer 0 w 9 such that w/10ⁿ⁺¹ y n+1 + 1/10_n+1.

b) Prove that given x ∊ [0, 1) there exist integers 0 x_k 9 such that for all n ∊ N,

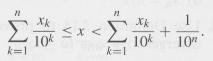
c) Prove that given x ∊ [0, 1) there exist integers 0 X_k 9, k ∊ N, such that

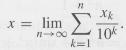
d) Using part c), prove that 0.5 = 0.4999... and 1 = 0.999....

7n tk 10% ' 10" 10% ! ! 1 x= lim