a. The simplest way to derive the Schwarz inequality goes as follows. First, observe ( + ? |? >) ? 0 for any complex number A; then choose A in such a way that the preceding inequality reduces to the Schwarz inequality.

b. Show that the equality sign in the generalized uncertainty relation holds if the state in question satisfies ?A| ? > = ?? B | ? > with ? purely imaginary.

c. Explicit calculations using the usual rules of wave mechanics show that the wave function for a Gaussian wave packet given by satisfies the minimum uncertainty relation Prove that the requirement = (imaginary number) is indeed satisfied for such a Gaussian wave packet, in agreement with (b).

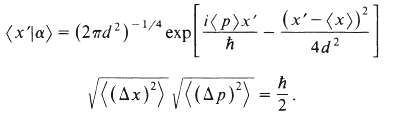
)x ('- (x)* 4d2 (*1) - (2nd?) " exp ") )") 2