According to the WLLN (Application 1 to Theorem 9), if the r.v.s X 1 ,...,X n are i.i.d. with finite X 1 , then The

According to the WLLN (Application 1 to Theorem 9), if the r.v.s X₁,...,X_n are i.i.d. with finite ԐX₁, then

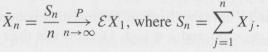
The following example shows that it is possible for {S_n/n} to converge in probability to a finite constant, as n → ∞, even if the ԐX₁ does not exist. To this effect, for j = 1, 2,..., let Xj be i.i.d. r.v.s such that P(Xj = -n) = P(Xj = n) = c/n² log n, n ≥ 3, where

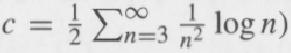
Then show that ԐX₁ does not exist, but

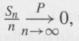
Where

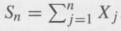
Show that ԐX₁ does not exist by showing that ԐX₁⁺ = ԐX₁^- = ∞. Next, set X_nj = X_j if |X_j| nj = 0 otherwise, j = 1,2…> 3, and let

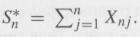
Then show that (i)

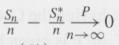
by showing that

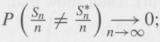
(ii) Ԑ(S^*_n/n) = 0

(iii)

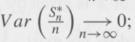
 (iii), conclude that

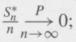
Then (i) and (iv) complete the proof.

In all Exercises 11-16, i is to be treated as a real number, subject, of course, to the requirement that i² = -1

Sn Sn P EX1, where S, = xj. , j=1