An ideal analog integrator is described by the system function H_a(s) = 1/s. A digital integrator with system function H(z) can obtained by use of the bilinear transformation. That is,

(a) Write the difference equation for the digital integrator relating the input x(n) to the output y(n).

(b) Roughly sketch the magnitude |H_a(j?)| and phase ?(?) of the analog integrator.

(c) It is easily verified that the frequency response of the digital integrator is roughly sketch |H(?)| and ?(?).

(d) Compare the magnitude and phase characteristics obtained in parts (b) and (c). How well does the digital integrator match the magnitude and phase characteristics of the analog integrator?

(e) The digital integrator has a pole at z = 1. If you implement this filter on a digital computer, what restrictions might you place on the input single sequence x(n) to avoid computational difficulties?

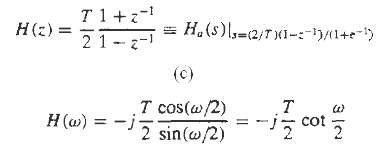
T 1+z- 21 - z- (c) T cos(w/2) 2 sin(@/2) H(2) = = H,(s),-2T)1-:-)(1+e-) -z cot H (a) = - 2