Another way to fill in the "missing link" in Fig. 5.48 is to look for a magnetostatic analog to Eq. 2.21. The obvious candidate would be

(a) Test this formula for the simplest possible case--uniform B (use the origin as your reference point). Is the result consistent with Prob. 5.247 You could cure this problem by throwing in a factor of ½, but the flaw in this equation runs deeper. 

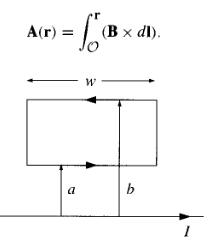
(b) Show that f(B x d1) is not independent of path, by calculating f(B x dl) around the rectangular loop shown in Fig. 5.63. 

As far as I know 19 the best one can do along these lines is the pair of equations 

(i) V(r) =  €“ r ˆ™ f₀¹ E(λr) dλ, 

(ii) A(r) = €“ r x f₀¹ λB (λr) dλ. 

[Equation (i) amounts to selecting a radial path for the integral in Eq. 2.21; equation (ii) constitutes a more "symmetrical" solution to Prob. 5.30.] 

(c) Use (ii) to find the vector potential for uniform B. 

(d) Use (ii) to find the vector potential of an infinite straight wire carrying a steady current 1. Does (ii) automatically satisfy ˆ† ˆ™ A = 0?

( d). A(r) =