Question: Show that if and only if there is a sequence 0 < e n 0 such that For the part e n 0, show that,
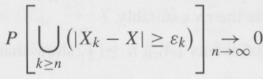
For the part en ![]() 0, show that, for every e > 0, there exists N = N(e) such that k ³ and n ³ imply
0, show that, for every e > 0, there exists N = N(e) such that k ³ and n ³ imply ![]() (|Xk €“ X| ³ e) Ã
(|Xk €“ X| ³ e) à ![]() (|Xk €“ X| ³ ek) and then use Theorem 4 suitably. For the part
(|Xk €“ X| ³ ek) and then use Theorem 4 suitably. For the part ![]() , use Theorem 4 in order to conclude that
, use Theorem 4 in order to conclude that
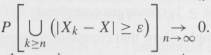
Applying this conclusion for m ³ 1, show that there exists a sequence nm †‘ ¥ as m †’ ¥ such that
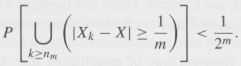
Finally, for nm £ k < nm +1, set ek = 1/m and show that
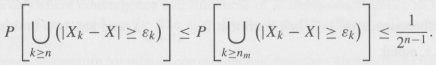
a.s. X "X
Step by Step Solution
3.32 Rating (164 Votes )
There are 3 Steps involved in it
First suppose that there exists n with 0 n 0 for which For every 0 there exists an integer k 0 such ... View full answer

Get step-by-step solutions from verified subject matter experts
Document Format (1 attachment)
742-M-S-P (6813).docx
120 KBs Word File


