Consider an arbitrary digital filter with transfer function?

(a) Perform a two-component polyphase decomposition of H(z) by grouping the even-numbered samples h₀(n) = h(2n) and the odd-numbered samples h₁(n) = h(2n +1). Thus show that H(z) can be expressed as:

H(z) = H₀(z²) + z^?1H₁(z²) and determine the H₀(z) and H₁(z).

(b) Generalized the result in part (a) by showing that H(z) can decomposed into an D-component polyphase filter structure with transfer function, Determine H_k(z).

(c) For the IIR filter with transfer function H(z) = 1/ 1?az^?1

Determine H₀(z) and H1(z) for the two-component decomposition.

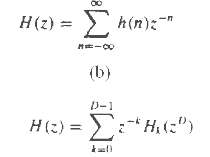
H(z) = h(n):-" (b) D-1 H(2) = :* H,(:") "H,(")