Question: Consider a particle in one dimension whose Hamiltonian is given by l*(E. - E.) = 2m alt=Consider a particle in one dimension whose Hamiltonian
Consider a particle in one dimension whose Hamiltonian is given by
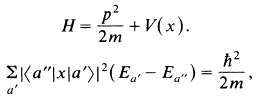l*(E. - E.) = 2m " alt="Consider a particle in one dimension whose Hamiltonian is given" class="fr-fic fr-dii">
By calculating [[H, x], x] prove where |a?> is an energy eigenket with eigenvalue E??.
p? +V(x). - 2m h? EKa"|x|a">l*(E. - E.) = 2m
Step by Step Solution
★★★★★
3.41 Rating (173 Votes )
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock
E x p2m Vx x 1Xm therefore x x K ... View full answer
Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock
Document Format (1 attachment)
28-P-M-P-Q-M (179).docx
120 KBs Word File
Study Help