Consider a potential well defined as U(x) = ? for x 0 for x > L (Fig. 40.27). Consider a particle with mass m and kinetic energy E (a) The boundary condition at the infinite wall (x = 0) is ?(0) = 0. What must the form of the function ? (x) for 0 (b) The wave function must remain finite as x ? ?. What must the form of the function ? (x) for x > L be in order to satisfy both the Schrodinger equation and this boundary condition at infinity?(c) Impose the boundary conditions that ? and d?/dx are continuous at x = L. Show that the energies of the allowed levels are obtained from solutions of the equation k cot kL = - K. where k = ?2mE/h and K = ?2m (U0 ?? E)h.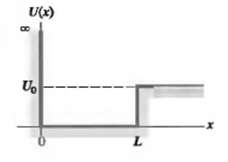

U(x) % 0 7 -x