Question: Consider, sampling from a multivariate normal distribution with mean vector = (1, 2, . . . , M) and covariance matrix 2I. The log-likelihood

Consider, sampling from a multivariate normal distribution with mean vector μ = (μ1, μ2, . . . , μM) and covariance matrix σ2I. The log-likelihood function is Show that the maximum likelihood estimates of the parameters are Derive the second derivatives matrix and show that the asymptotic covariance matrix for the maximum likelihood estimators is Suppose that we wished to test the hypothesis that the means of the Mdistributions were all equal to a particular value μ0. Show that the Wald statistic would be where ?y is the vector of sample means.br>

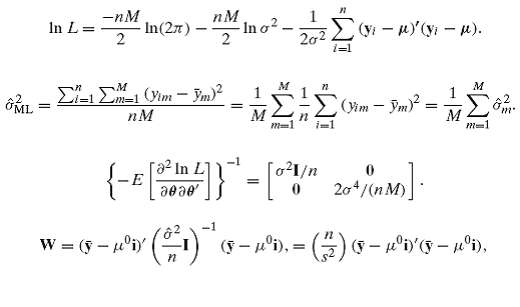
OML In L= = -nM N/3 2 In(27) - - nM 2

OML In L= = -nM N/3 2 In(27) - - nM 2 Ino -1 M-1 (Yim - Ym) m=1 nM = W = ( - nv (21) M M M1 20 In L {-E [2001]} = [0/ . 72 11 -( ). 1=1 n (x-i), = ( (yim - Ym) 20+ / M)] = M M M1 ) ( i)' (y i), 'm'

Step by Step Solution

★★★★★

3.35 Rating (161 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Consider sampling from a multivariate normal distribution with mean vector and covariance matrix I T... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

3-M-E-E-A (131).docx

120 KBs Word File

Students Have Also Explored These Related Econometric Questions!

Consider sampling from a multivariate normal distribution with mean vector = ( 1 , 2 , . . . , M ) and covariance matrix 2 I. The log-likelihood function is Show that the maximum likelihood...

Consider a normal distribution with mean 0. Use your graphing calculator or geometry software to explore how the standard deviation, , affects the equation of the normal curve, Summarize how the...

Consider a normal distribution with mean 0. You've already seen that the equation of the normal curve is To avoid using e, you can use another equation that approximates the normal curve: Use your...

please with details,thank you 3. (a) Partition the random vector X, and its covariance matrix E, as follows: X = X1 Ell E12 X 2 E = E21 _22 Assuming Ezz is non-singular, define Y = X1 - E12Ez X2 Y2 X...

3 In 0900'0 500O'D 1000 0 FIG. 4. Process H alloy composition: (a) & chart, (b) "chart based on log ratios, (o) X' versus 73. S 0900'0 50COD 100070 S602 R. A. Boyles For this data set, step (3) in...

1. What percentage of the Nobel laureates were women? Construct a pie chart which shows how many prizes went to men compared to how many prizes went to women. Present your findings

q: I need help with question 13, the picture attached, please! tell me if the question is not clear. 13. Let (X 15, X2011, 2' = 1, . - - , n, be iid random vectors from a bivariate normal...

I need hint or answer of PROBLEM 3 a and b. PROBLEM 3 Answer the following questions: a. Suppose X1, X2, X3, X4 are i.i.d. random variables N(0, ). Let Q = X1X2 - X3X4. By finding the moment...

Question 9 6.2 The Standard Normal Distribution Table: Z-score and Probability A manufacturer knows that their items have a normally distributed lifespan, with a mean of 7.6 years, and standard...

6 The Multivariate Normal Distribution The multivariate normal distribution with mean R d and positive definite covariance matrix R dd , denoted N(, ), has the probability density function f(x; , ) =...

What is meant by the critical region? The noncritical region?

Triangle Fastener Corporation accumulates costs for its single product using process costing. Direct material is added at the beginning of the production process. and conversion activity occurs...

Which 2 of these could you select to start a payroll run?Select all that apply, and then select Submit. The Run payroll button in the Dashboard option from the left - hand navigation The Payroll...

We are analyzing 2 products product Hamburgers(HB)and Double Deckers(DD) Product HB requires 1 Patty (P) and 2 Buns (B) Product Y requires 2 Patties (P) and 3 Buns B) The standard cost for P is $1...

P1. Coyote Company manufactures and sells 2 products: EL and GL. Coyote uses a job-order costing system in which overhead is applied to jobs on the basis of machine hours. Its predetermined overhead...

Write a note on Health care organization and briefly evaluating the following Interdepartmental interaction, communications, team building activities and conflict resolution techniques, ethics and...

A man decided to paint his house himself after office hours. He can paint 25 m2 per hour on average. It takes him 15 mins to prepare his materials and 20 minutes to keep the materials after painting....

An active fixed-income manager is considering two corporate bond positions for an active portfolio. The first bond has a BBB rating with a credit spread of 2.75% and an effective spread duration of...

Unbiased estimates of the variance components: The one-way model. Using (2.21) and (2.22), show that $E\left(\widehat{\sigma}_{1}^{2}ight)=\sigma_{1}^{2}$ and...

Fuller and Battese (1973) transformation for the one-way random effects model. (a) Verify (2.17) and check that $\Omega^{-1} \Omega=I$ using (2.18). (b) Verify that \(\Omega^{-1 / 2} \Omega^{-1 /...

For the gasoline data given as Gasoline.dat on the Springer website, verify the testing for the poolability results given in example 2, Sect.4.1.3.

For Grunfeld's data given as Grunfeld.fil on the Springer website, verify the testing for the poolability results given in example 1, Sect.4.1.3.

Verify that $\dot{M}$ and $\dot{M}^{*}$ defined below (4.10) are both symmetric, idempotent, and satisfy $\dot{M} \dot{M}^{*}=\dot{M}^{*}$. = *8* + (4.10)

Chapter 10 - HW Table 1 1. Given the information in Table 1 and 15 percent cost of capital, (a) Compute the net present value & IRR (b) Should the project be accepted? 2. Use the IRR approach to...