Consider the equation below that gives interest rate dynamics in a setting where the time axis [0, T] is subdivided into it equal intervals, each of length ?:

r_t+? = r_t + ?r_t + ?_t(W_t+? ? W_t) + ?₂(W_t ? W_t??)

where the random error terms

?W_t = (W_t+? - W_t)

are distributed normally as

?W_t ? N (0,?(?)).

(a) Explain the structure of the error terms in this equation. In particular, do you find it plausible that ?W_t-? may enter the dynamics of observed interest rates?

(b) Can you write a stochastic differential equation that will be the analog of this in continuous time? What is the difficulty?

(e) Now suppose you know, in addition, that long-term interest rates, R, move according to a dynamic given by

R_t+? = R_t + ?r_t + ?₁(W_t+? ? W_t) + ?₂(W_t ? W_t??),

where we also know the covariance:

E[?W?W] = ??.

Can you write a representation for the vector process

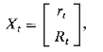
such that Xt is a first-order Markov?(d) Can you write a continuous lime equivalent of this system?(e) Suppose short or long rates are individually non-Markov. Is it possible that they are jointly so?

, 3D R.