Consider the following problem.

Maximize Z = 2x₁ – x₂ + x₃,

Subject to

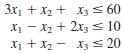
and

x₁ ≥ 0, x₂ ≥ 0, x₃ ≥ 0.

After slack variables are introduced and then one complete iteration of the simplex method is performed, the following simplex tableau is obtained.

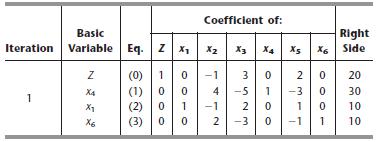
(a) Identify the CPF solution obtained at iteration 1.

(b) Identify the constraint boundary equations that define this CPF solution.

3x1 + x2 + x3 60 X1 + X2 20 Coefficlent of: Basic Right Iteration Varlable Eq. Zx3 Side Z (0) 03 0 20 20 (1) 0 04-5 3030 x(2) 2 00 10 x6(3) 0 023 0 10