Consider the following problem.

Maximize Z = 4x₁ + 3x₂ + x₃ + 2x₄,

Subject to

and

x₁ ≥ 0, x₂ ≥ 0, x₃ ≥ 0, x₄ ≥ 0.

Let x₅ and x₆ denote the slack variables for the respective constraints. After you apply the simplex method, a portion of the final simplex tableau is as follows:

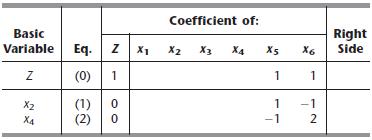
(a) Use the fundamental insight presented in Sec. 5.3 to identify the missing numbers in the final simplex tableau. Show your calculations.

(b) Identify the defining equations of the CPF solution corresponding to the optimal BF solution in the final simplex tableau.

3x223 s4 Coefficient of: Right VariableEq. ZX1 x2 X3 x4 X5 Side Basic #11 (0) 1 x2 1) 0 4(2) 0 1-1 -1 2