Consider the four 3 × 3 linear systems having the same coefficient matrix:

2x₁ − 3x₂ + x₃ = 2, 2x₁ − 3x₂ + x₃ = 6,

x₁ + x₂ − x₃ = −1, x₁ + x₂ − x₃ = 4,

−x₁ + x₂ − 3x₃ = 0; −x₁ + x₂ − 3x₃ = 5;

2x₁ − 3x₂ + x₃ = 0, 2x₁ − 3x₂ + x₃ = −1,

x₁ + x₂ − x₃ = 1, x₁ + x₂ − x₃ = 0,

−x₁ + x₂ − 3x₃ = −3; −x₁ + x₂ − 3x₃ = 0.

a. Solve the linear systems by applying Gaussian elimination to the augmented matrix

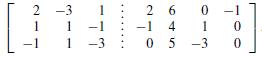
b. Solve the linear systems by finding and multiplying by the inverse of

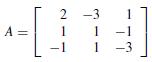
-3 1:26 0-1 -1 :-1 4 -3 : 0 5-3 0 2 -3 1 A=| | 1-1 1 1-3