Consider the Green function appropriate for Neumann boundary conditions for the volume V between the concentric spherical surfaces defined by r = a and r = b, a

Where g_t(r, r') = r^l_{/ r^l+1>?+ f^l(r, r')}

(a) Show that for l > 0, the radial Green function has the symmetric form

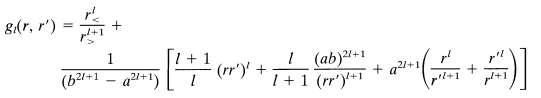
(b) Show that for l = 0

Where f?(r) is arbitrary. Show explicitly in (1.46) that answers for the potential ?(?) are independent of f(r).

[The arbitrariness in the Neumann Green function can be removed by symmetrizing g₀ m r and r' with a suitable choice of f(r).]?

G(x, x') = 8(r. r")P(cos y) 1=0