Consider the measurable space (W, A) and let A n A, n = 1, 2, then recall that And (i) Show that A n

Consider the measurable space (W, A) and let A_nˆˆ A, n = 1, 2,€¦ then recall that

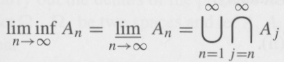
And

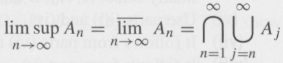
(i) Show that  A_n  A_n. (If also  A_n  A_n€™ so that  A_n = _n†’ˆžA_n€™ then this set is denoted by  A_n and is called the limit of the sequence {A_n}, n ‰¥ 1.

(ii) Show that ( A_n) = _n†’ˆž A^c_n ( A_n)c = _n†’ˆž A^c_n conclude that if lim _n†’¥ A_n = A, then lim _n†’¥ A^c_n = A^c.

(iii) Show that

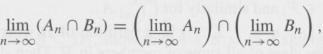
And

(iv) Show that

And

(v) By a counterexample, show that the inverse inclusions in part (iv) do not hold, so that _n†’ˆž (A_n È B_n) need not be equal to (_n†’ˆž A_n) Ç (_n†’ˆž B_n), andA_n (A_n È B_n) need not be equal to (A_n) È (B_n).

(vi) If lim_n†’¥ A_n = A and lim_n†’¥ B_{n =} B_, then show that lim_n†’¥ (A_n Ç B_n) = A Ç B and lim_n†’¥ (A_n È B_n) = A È B.

(vii) If lim_n†’¥ A_n = A, then show that for any set B, lim_n†’¥ (A_n DB) = ADB. where A_n D B is the symmetric difference of A_n and B.

(viii) If A_2j€“1 = B and A_2j = C, j = 1, 2, €¦, determine A_n and n†’ˆžA_n. Under what condition on B and C does the limit exist, and what is it equal to?

lim inf A, = lim A, =UNA n=1 j=n %3D n 00