Consider the probability space (W,A,P), and let Q be an open subset of Â. Let g(×; ×) : W ´ Q †’  be (A´B_Q) €“ measurable, where B_Qis the s-field of Borel subsets of Q, we say that g(×;q) is differentiable in q.m. atq, if there exits a (A´B_Q)-measurable functiong(×;q) (the quadratic mean derivative ofg(×;q) atq) such that

Now let p(x; q) = ½ e ^{€“  |x €“ q|}, x ÃŽ  (q ÃŽ Â) to be double exponential probability density function, and for q, q* ÃŽ Â, Set

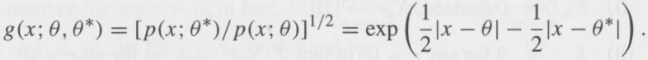
(i) Show that g(x; q, q*) is not ponitwise differentiable with respect to q* at (q, q) for any q = x Î Â.

(ii) If the r.v. x is distributed according to p(×; q), show that g(X; q, q*) is differentiable in qm. With respect to q* at (q, q) Î Â, with q.m. derivative g(X;q) given by:

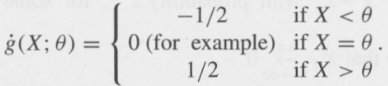
h-[g(;; 0 + h) g(;; 0)] q.m. g(;; 0).