Consider the Proca equations for a localized steady-state distribution of current that has only a static magnetic moment. This model can be used to study the observable effects of a finite photon mass on the earth's magnetic field. Note that if the magnetization is M(x) the current density can be written as J = c(? ?M).

(a) Show that if M = mf(x), where m is a fixed vector and?f(x) is a localized scalar function, the vector potential is

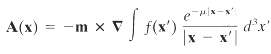
(b) If the magnetic dipole is a point dipole at the origin [f(x) = ?(x)], show that the magnetic field away from the origin is

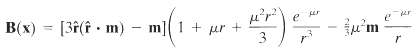
(c) The result of part b shows that at fixed r = R (on the surface of the earth), the earth's magnetic field will appear as a dipole angular distribution, plus an added constant magnetic field (an apparently external field) antiparallel to m. Satellite and surface observations lead to the conclusion that this "external" field is less than 4 ? 10^?3 times the dipole field at the magnetic equator. Estimate a lower limit on ?^?1 in earth radii and an upper limit on the photon mass in grams from this datum.

A(x) eHix- -m x x - x'| d'x'