Creeping flow between two concentric spheres (Fig. 3B.4). A very viscous Newtonian fluid flows in the space between two concentric spheres, as shown in the figure. It is desired to find the rate of flow in the system as a function of the imposed pressure difference. Neglect end effects and postulate that v_θ depends only on r and θ with the other velocity components zero. 

(a) Using the equation of continuity, show that v_θ sin θ = u(r), where u(r) is a function of r to be determined. 

(b) Write the θ-component of the equation of motion for this system, assuming the flow to be slow enough that the [v ∙ ∆v] term is negligible. Show that this gives   

(c) Separate this into two equations where B is the separation constant, and solve the two equations to get where P₁ and P₂ are the values of the modified pressure at θ = ε and θ = π – ε, respectively. 

(d) Use the results above to get the mass rate of flow

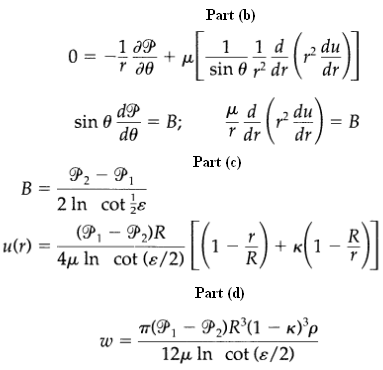
Part (b) 2 du dr 1 aP 1 d sin 0 y dr 0 = () - B dP du dr r dr sin e - B; Part (c) P2 B = P1 2 In cot e (P, P2)R 4 In cot (8/2) (r) Part (d) 7(P, P2)R(1 K)'p 12 1n cot (/2)