Question: Differentiating with respect to the expressions on both sides of the equation Show that the mean of the geometric distribution is given by

Differentiating with respect to θ the expressions on both sides of the equation

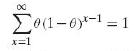
0a-or-1-1

Show that the mean of the geometric distribution is given by µ = 1/θ. Then, differentiating again with respect to θ, show that µ'₂ = 2 – θ / θ² and hence that σ² = 1 – θ / θ².

0a-or-1-1

Step by Step Solution

★★★★★

3.31 Rating (166 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Then differentiate twice with res... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Document Format (1 attachment)

583-S-J-P-D (784).docx

120 KBs Word File

Students Have Also Explored These Related Statistics Questions!

Differentiating with respect to Î» the expressions on both sides of the equation Derive the following recursion formula for the moments about the mean of the Poisson distribution: For r =...

Consider the log likelihood for the linear-by-linear association model. a. Differentiating with respect to Î² and evaluating at Î² = 0 and null estimates of parameters, show...

The information about in a random sample of size n is also given by Where f (x) is the value of the population density at x, provided that the extremes of the region for which f(x) 0 do not depend...

2 2 . Differentiating with respect to the expressions on both sides of the equation ' q x = 1 ( 1 ) x 1 = 1 show that the mean of the geometric distribution is given by = 1 . Then, differentiating...

1 This assignment covers material from Units 1 to 4 in the Mathematics 244 Study Guide. It is due after Unit 4 in the Study Guide is completed. Total Marks = 150 1. Evaluate each of the following...

E Test: Chapter 5 Test Question list 0 Question 1 0 Question 2 0 Question 3 0 Question 4 0 Question 5 0 Question 6 0 Question 7 0 Question 8 I? Find the anlidelivative utthe given derivative do (X +...

A. B. A. B. ( ( ) ) Beginning and Intermediate Algebra An open source (CC-BY) textbook Available for free download at: http://wallace.ccfaculty.org/book/book.html by Tyler Wallace 1 ISBN...

unit II q12. Summarized on the right is the sale (in thousands) of the top five products in 2002. Use this information to calculate what percent of the sales of these five products was due to product...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

In this question you will be asked to reflect on a project you have been involved in or observed, in which a design evolved, or could have evolved, through applying a theory of user behaviour. You...

Monica and Samantha, both South African residents, have been friends since kindergarten. They attended university together and both became successful businesswoman. With the tourism industry booming...

Name the muscles of the posterior muscular system. Muscular System: Posterior 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. LiteART Collection Images Copyright 1989-2001...

Abels, a company established in the Netherlands, sells to Bartels, a company established in Germany, a number of radios at a price of 1 5 0 , 0 0 0 Euros. The moment they are delivered to Bartels it...

The euro area: a) does not need to coordinate its monetary policy with national fiscal policies; b) experienced a financial crisis because of the US subprime bubble; c) has an orderly-working...

A company that manufactures toothpaste is studying five different package designs. Assuming that one design is just as likely to be selected by a consumer as any other design, what selection...

Data on U.S. work-related fatalities by cause follow (The World Almanac, 2012). Cause of Fatality Number of Fatalities Transportation incidents ............. 1795 Assaults and violent acts...

The Taylors agreed to make monthly payments on a mortgage of $142,000 amortized over 15 years. Interest for the first 3 years was 6.5 percent compounded semi-annually. Determine the mortgage balance...

WACC Comprehensive A company has a proposed 2-year project with the cash flows shown below and would like to calculate the NPV of this project so that they can decide whether to pursue the project or...

Dada la siguiente informacin, calcule el WACC para Stigum Inc. Suponga que la empresa tiene una tasa impositiva del 35%. Deuda : 220.000 bonos en circulacin con una tasa de cupn del 3,5%. Valor...