Doping changes the Fermi energy of a semiconductor. Consider silicon, with a gap of 1.11 eV between the top of the valence band and the bottom of the conduction band. At 300 K the Fermi level of the pure material is nearly at the mid-point of the gap. Suppose that silicon is doped with donor atoms, each of which has a state 0.15 eV below the bottom of the silicon conduction band, and suppose further that doping raises the Fermi level to 0.11 eV below the bottom of that band (Figure). For(a) Pure and(b) Doped silicon, calculate the probability that a state at the bottom of the silicon conduction band is occupied.(c) Calculate the probability that a state in the doped material isoccupied.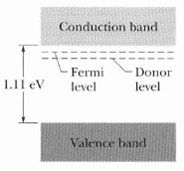

Conduction band Fermi Donor 1.11 eV level level Valence band