For n ‰¥ l, let X_n, Y_n and X, Y be r.v.s defined on the probability space (Ω, A, P), let d₁, d₂and c_nbe constants with 0 ‰  c_n†’ ˆž as n †’ ˆž, and suppose that

Let g: R² †’ R be differentiable, and suppose its (first-order) partial derivatives g_x, g_y are continuous at (d₁, d₂). Then show that, as n †’ ˆž,

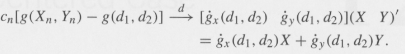
| Cn (Xn d1, Yn dz)$(x, ) as n n oO.