For the special case ux = 0, the transverse velocity addition formula, equation (10.35), yields uy = uy/?. Derive this in the following way. In frame S??, a particle moves with speed u?? in the y??-direction. Frame S moves to the left with speed v, so that the situation in S looks like that in Figure, with the y-speed now u. Consider a series of equally spaced dotted lines, as shown. The ratio of times between passes of the dotted lines in frames S and S?? is TS/TS?? = (1/u) / (1/u) = u??/u. Derive another expression for this ratio by using time dilation arguments, and then equate the two expressions to solve for u in terms of u?? and v.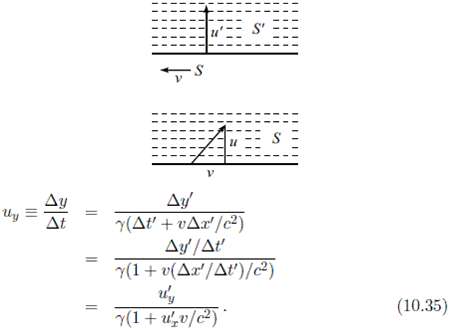

Ay Uy = At (At' + vAr'/c2) Ay/At Y(1+ v(Ar'/At')/c2) (10.35) Y(1+ uv/c)