Given x 1 and x 2 distributions that are normal or approximately normal with unknown 1 and 2 , the value of t

Given x₁ and x₂ distributions that are normal or approximately normal with unknown σ₁ and σ₂, the value of t corresponding to x̅₁ –­ x̅₂ has a distribution that is approximated by a Student’s t distribution. We use the convention that the degrees of freedom are approximately the smaller of n₁ – 1 and n₂ –­ 1. However, a more accurate estimate for the appropriate degrees of freedom is given by Satterthwaite’s formula

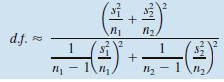
where s₁, s₂, n₁, and n₂ are the respective sample standard deviations and sample sizes of independent random samples from the x₁ and x₂ distributions. This is the approximation used by most statistical software. When both n₁ and n₂ are 5 or larger, it is quite accurate. The degrees of freedom computed from this formula are either truncated or not rounded.

(a) Use the data of Problem 14 (weights of pro football and pro basketball players) to compute d.f. using the formula. Compare the result to 36, the value generated by Minitab. Did Minitab truncate?

(b) Compute a 99% con­fidence interval using d.f.

ni 2 df. L+ TL 97 97