Engineering
Telecommunication Engineering
Harmonic distortion in digital sinusoidal generators an ideal sinusoidal generator

Harmonic distortion in digital sinusoidal generators an ideal sinusoidal generator produces the signal x(n) = cos2?f0n -?

Question:

Harmonic distortion in digital sinusoidal generators an ideal sinusoidal generator produces the signal x(n) = cos2?f0n -? Total power(a) Show that(b) By using the Taylor approximation compute one period of x (n) for f0 = 1/96, 1/32, 1/256 by increasing the number of terms in the Taylor expansion form 2 to 8.(c) Compute the THD and plot the power density spectrum for each sinusoid in part (b) as well as for the sinusoids obtained using the computer cosine function. Comment on the results.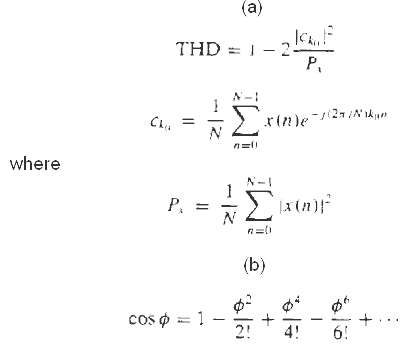

Transcribed Image Text:

(a) THD = 1- 2- P, Σεme > r(n)e 2 IN kan n= where N- 2(n) (b) cos = 1 - 2! 4! 6!

Fantastic news! We've Found the answer you've been seeking!

Step by Step Answer:

Answer rating: 87% (8 reviews)

a b For f 0 196 refer to figure For f 0 132 refer to figure For f 0 1256 refe...View the full answer

Answered By

Utsab mitra

I have the expertise to deliver these subjects to college and higher-level students. The services would involve only solving assignments, homework help, and others. I have experience in delivering these subjects for the last 6 years on a freelancing basis in different companies around the globe. I am CMA certified and CGMA UK. I have professional experience of 18 years in the industry involved in the manufacturing company and IT implementation experience of over 12 years. I have delivered this help to students effortlessly, which is essential to give the students a good grade in their studies.

3.50+ 2+ Reviews 10+ Question Solved

Related Book For book-img-for-question

Digital Signal Processing

ISBN: ?978-0133737622

3rd Edition

Authors: Jonh G. Proakis, Dimitris G.Manolakis

See More Books

Question Posted: May 26, 2011 02:58 AM

See More Questions

Students also viewed these Telecommunication Engineering questions

An AC power generator produces 50 A (rms) at 3,600 V. The voltage is stepped up to 100,000 V by an ideal transformer, and the energy is transmitted through a long-distance power line that has a...
Compute E[X] if X has a density function given by (a) (b) (c) f(x) = 4 otherwise x)c) -1 x 1 otherwise
The power spectrum at the input to an ideal BPF is Let the transfer function for the ideal BPF be Determine the autocorrelation function of the output. You may have to make a reasonable approximation...
Refer to Figure 14.3. Select a year when the gallons of oil spilled were over 15 million. Research the spill(s) for that year. Was the amount due to one oil spill or multiple oil spills?Investigate...
In the year 2012, a real estate analyst forecasts that a rental apartment building will generate $5.3 million each year in rent over the five years 2013- 2017. Cash expenses are expected to be $4.2...
The following costs were incurred by Osaka Metals Company to maintain the quality of its products. (Yen is the national currency of Japan.) 1. Operating an X-ray machine to detect faulty welds,...
Describe parasite drag.
Bonnie died on June 1, 2015, survived by her husband, Abner, and two sons, Carl and Doug. Bonnies only lifetime taxable gift was made in October 2013 in the taxable amount of $6.25 million. She did...
How would you help employees build cultural intelligence in your fictional organization? Name and explain two specific actions you would take to help employees build cultural intelligence. Explain...
Kerron owns a shop supplying fishing tackle. During March 2014 he returned goods to suppliers that had previously been purchased on credit. Prepare the following accounting records to record these...
Consider the filter y(n) = 0.9y (n 1) + bx (n) (a) Determine b so that |H(0) = 1.| (b) Determine the frequency at which |H()| = 1/2. (c) Is this filter low pass, band pass, or high pass? (d) Repeat...
Measurement of the total harmonic distortion in quantized sinusoids let x(n) be a periodic sinusoidal signal with frequency f0 = k/N, that is, x(n) = sin 2 f0n. (a) Write a computer program that...
The Federal Food Stamp Act provided for the distribution of food stamps to needy households. In 1971, section 3(e) of the statute was amended to define households as limited to groups whose members...
What is the output of the following C program when it is run as "a.out 1 2 3"? 4 5 7 MAS698 1 #include 2 9 10 11 12 13 } } #include int yMethod(int a[]) { a-(4,5,6,7,8); return...
Prepare a schedule C for the following cases: Case 1: Carmelo Mendez Carmelo Mndez is married and has a car stereo business. Total sales for this taxable year were $75,000. Carmelo had the following...
Current Period Revenues Construction Expenses Materials Labor Subcontract Equipment Income Statement Other Total Construction Expenses Equipment Expenses Rent and Lease Payments Depreciation Repairs...
The following information is for Kon Inc. for the year ended December 31, 2021: Common shares, Jan. 1 $20,000 Common shares issued during year 10,000 Retained earnings, Jan. 1 58,000 Office expense...
1. Draw a free body diagram for a pole vaulter: a. The athlete. Assume that ax < 0, ay > 0. Please note I have indicated the forces on the athlete at their front hand. (2) b. The pole. Assume ax < 0,...
The mathematical model of a nonlinear system is provided. Using the procedure outlined in this section, find the operating point and derive the linearized model. \(\begin{cases}\dot{x}_{1}=-x_{1}+3...
In a nonmagnetic medium, E = 50 cos (10 9 t 8x) a y + 40 sin (10 9 t 8x) a z V/m find the dielectric constant r and the corresponding H.
For the reaction 2 NO(g) + Cl 2 (g) 2 NOCl(g), K c = 3.7 x 10 8 at 298 K. In a 1.50 L flask, there are 4.125 mol of NOCl and 0.1125 mol of Cl 2 present at equilibrium (298 K). (a) Determine the...
Let H{?} denote the (ideal) operation of Hilbert transformation; that is, Prove the following properties of the ideal Hilbert transform operator. Hx[n}} = x[k]h[n - k], [[u]x}H k=-o0 where h[n] is 2...
An ideal Hilbert transformer with impulse response has input x r [n] and output x i [n] = x r [n] * h[n], where x r [n] is a discrete-time random signal. (a) Find an expression for the...
In Section 11.3, we mention that a causal complex cepstrum x[n] is equivalent to the minimum-phase condition of Section 5.4. Remember that x[n] is the inverse Fourier transform of X(e j? ) as defined...
Last year, a city had three school districts: North with a population of 5200 children, South with a population of 10600 children, West, with a population of 15100 children. Use Hamilton, Adams,...
Prepare the journal entry to record pension expense and the employer ? s contribution to the pension plan in 2 0 2 0 . ( Credit account titles are automatically indented when amount is entered. Do...
Concord Department Store uses a perpetual inventory system. Data for product E2-D2 include the following purchases. Date Number of Units Unit Cost May 7 July 28 45 30 $13 15 On June 1, Concord sold...

Understanding And Auditing Corporate Culture A Maturity Model Approach 1st Edition - ISBN: 1634540719 - Free Book

Study smarter with the SolutionInn App