In Example 24-12 you derived the expression for the potential inside a solid sphere of constant charge density by first finding the electric field. In this problem you derive the same expression by direct integration. Consider a sphere of radius R containing a charge Q uniformly distributed. You wish to find V at some point r

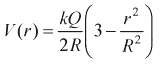
(a) Find the charge q? inside a sphere of radius r?and the potential V₁ at r?due to this part of the charge.

(b) Find the potential dV₂ at r?due to the charge in a shell of radius r? and thickness dr? at r? > r.

(c) Integrate your expression in (b) from r? = r?to r? = R?to find V₂.

(d) Find the total potential V?at r?from V?= V₁ + V₂.

Transcribed Image Text:

kQ V(r)%D (r)%3D 3- R? 2R