Let X be a r.v. having the Cauchy distribution with parameters μ = 0 and Ï = 1 (i.e., the p.d.f. of X is given

Let X be a r.v. having the Cauchy distribution with parameters μ = 0 and σ = 1 (i.e., the p.d.f. of X is given by p(x) = 1/Ï€ x 1/(1+x²) x ÃŽ R) Then show that:

(i) The EX does not exist.

(ii) The ch.f. fx(t) = e^-|t| t ˆˆ R.

Next, let X_1€¦.,X_n be independent r.v.s distributed as X and set S_n = X1 +€¦+ X_n. Then

(iii) Identify the ch.f. f_Sn(t).

(iv) Show that

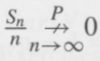
0 by showing that

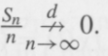
Although, by intuition, one would expect such a convergence, because of symmetry about 0 of the Cauchy distribution! For part (ii), use the result

(see, e.g., integral 403 in Tallarida (1999); also see integral 635 in the same reference).

Sn . 00