Question: Let X 1 , X 2 , . . . , X n denote the outcomes of a series of n independent trials, where for
Let X1, X2, . . . , Xn denote the outcomes of a series of n independent trials, where
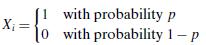
for i =1, 2, . . . , n. Let X = X1 + X2 +・ ・ ・+ Xn.
(a) Show that p̂1 = X1 and p̂2 = X/n are unbiased estimators for p.
(b) Intuitively, p̂2 is a better estimator than p̂1 because p̂1 fails to include any of the information about the parameter contained in trials 2 through n. Verify that speculation by comparing the variances of p̂1 and p̂2.
1 with probabilityp 0 with probability 1 p
Step by Step Solution
3.52 Rating (169 Votes )
There are 3 Steps involved in it
a EP i EX 1 p since X 1 is binomial wi... View full answer

Get step-by-step solutions from verified subject matter experts
Document Format (1 attachment)
681-M-C-M-S (833).docx
120 KBs Word File


